For the final week of the Explore MTBoS challenge, I am going to share my lesson on Absolute Value Functions written in piecewise notation.

Learning Target for Students: I will be able to write the equation of an absolute value function using piecewise notation.
At this point, we have spent many days graphing absolute value functions from tables and directly from examining the vertex form equation. We have also discussed the characteristics of absolute value functions.
When students entered the classroom, this warm up problem was posed to them:
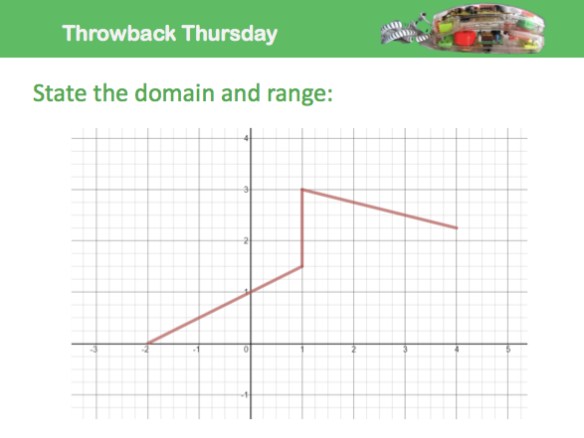
I chose this problem as our “throwback” because I wanted students to recall how to find the domain and range for a relation, since this skill would be necessary for today’s lesson involving the domain intervals for the pieces of the functions. After giving students a couple minutes to think about their answer, I switched up the problem so that the third segment had an arrow at the end; this allowed us to talk about how the domain and range would change if the line continued on forever.
At this point, I gave each student his/her own graph (I quickly removed extras once I had taken attendance for each class period. Only one class had an odd number of students, so I partnered up someone who been absent for 2 days with another student.) Here are the 20 that I pre-made:
I asked students to examine their graph, and briefly examine the graphs around them. What is similar about your graphs (linear, slopes, restricted domains)? What is different (slopes, y-intercepts, equations)? Students copied their own graph onto this sheet, in the box labeled: “My Linear Function.”
Students wrote the equation for their line, and determined its domain. Then I told students that right now, they were alone. Their graph was alone. But that somewhere out there, it has a perfect match. I showed students how if they folded the graph at the x-value of the domain interval, they would be able to line it up with another classmate’s graph, to create a new function. I directed students to find their match, and sit with their new partner.
Original graphs:
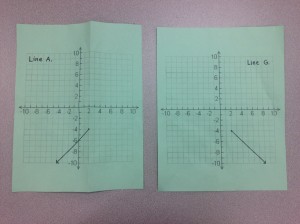
Post folding:
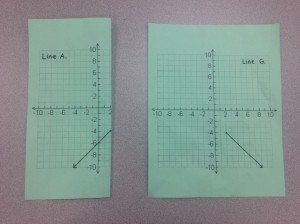
With perfect match:
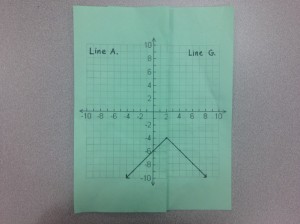
Students then shared everything they knew about their original line with their partner, and transferred the new information into the box: “My Partner’s Linear Function.” At this time, I asked students to recall earlier in the year when we studied piecewise linear functions, and how they were able to write the equation of each line segment. We talked about how they had not noticed that an absolute value function could be thought of as a composition of two linear pieces, until this moment. We talked about how easy they found it to write the equation for their individual piece, and it wasn’t much different adding in their partner’s piece. Students combined all the information to create “Our Absolute Value Function” and made observations about the two different forms the equations could be written. Most students recognized the the connection between the y-intercepts from piecewise notation as being the distance from the vertex (h units away from k).
When we tried another problem, I gave out yellow post-its so that students could hide part of the function, and focus on one line at a time. Some students prefer to use colored pencils to highlight the different pieces, so I also encourage this option.
I had every intention of giving students this exit ticket at the end of the period, but time ran away from us and I didn’t want to cut our earlier conversations short.
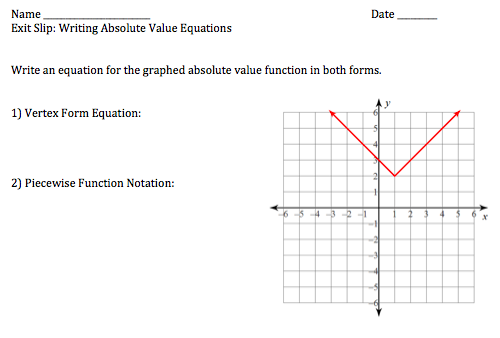
This is the second time I’ve attempted this activity, and I would do it again next year. I love how student pairs are determined by who is their perfect match, which gets my students to work with someone they usually don’t, and they know it’s completely random. I love how it’s close to Valentine’s Day, so we had a silly time with the idea of the Perfect Graph Match. I love how each student physically started out with only one line, and then did some paper folding to pair them with another. I love how this visual representation really shows the separation of the pieces, and that it’s a shared experience we can refer back to during the rest of the unit. And I love how it starts by activating students’ prior knowledge about lines, and how they could use that information in this new setting.
Would love to hear any feedback about this lesson, and if you try it in your room, please let me know how it goes!

